常用类

VirtualUniverse类、Locale类与HiResCoord类之间的关系

Virtual Universe 包含 Locale 包含 BranchGroup

每一个Locale对象都具有一个高分辨率大尺度坐标系，每一个Locale对象的高分辨率大尺度坐标系都用3个高分辨率大尺度数来定义其原点的坐标值x,y,z（用HiResCoord类定义）。

VirtualUniverse类定义的对象是包含所有场景图的最高级别的容器。

SimpleUniverse类

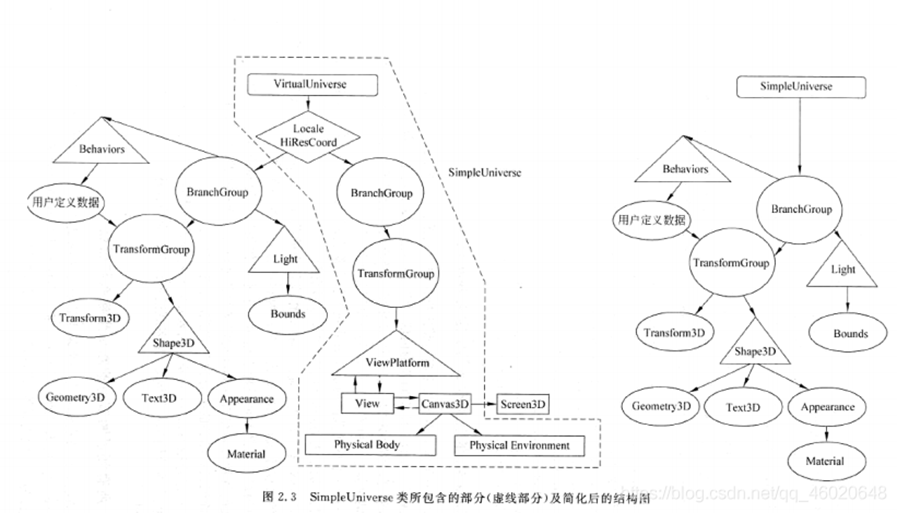
该类可快速地设置一个最小的用户环境，并且很容易使一个Java3D应用程序运行起来。该实用程序类创建了场景图中与观察相关的所有必须对象。该类创建了一个Locale, 一个单独的ViewingPlatform和一个Viewer观察者对象。但此类不适合复杂应用程序。

SimpleUniverse 包含 Locale 包含 BranchGroup 包含 TransformGroup 包含ViewPlatform

Bounds类

用于限定特定操作的作用范围

用于确定某种动作或行为的范围。

用于确定某种全景操作的应用范围

SharedGroup类

共享子图。SharedGroup节点作为共享子图的根节点。Link叶子节点链接向该SharedGroup节点，并不是将共享子图集成到当前场景图中。一个SharedGroup节点允许多个Link叶子节点同时通过链接的方式共享该子图。

View类

观察模型。应用Java3D观察模型编写的应用程序在不修改场景图的情况下，能够将可视化后的图像显示到各种不同的显示设备上

“一次编写到处运行”

ViewPlatform类

在虚拟世界中的观察平台。一个ViewPlatform叶子节点在虚拟世界中定义了一个坐标系和一个具有相关原点或参考点的参考框架。ViewPlatform作为观察对象的依附点，并且其作为一个可视化器观察的基点。

ViewingPlatform类

Java3D的三种坐标系：世界坐标系，观察坐标系，显示器坐标系

透视投影：当给定视点、观察方向与投影平面后，将世界坐标系转换为观察坐标系，对观察坐标系中的三维物体通过比例变换向投影平面投影。

平行投影：将空间的三维形体分别向3个坐标平面进行平行投影，分别形成主视图、俯视图与侧视图。

Shape3D类

Shaped3D类定义所有的几何体。它包含几何体与该几何体的外观属性。

几何体部分定义三维空间体的几何形状，外观属性部分定义颜色、材质等属性。

一个Shaped3D类包含一个Geometry几何组件列表和唯一一个Appearance外观组件对象。P55

Appearance类

定义所有与显示相关的外观状态，这些状态可设置为一个Shaped3D节点的组件对象。

Appearance类包含ColoringAttributes类，PointAttributes类，LineAttributes类，PolygonAttributes类，Rendering Attributes类，Transparency Attributes，Material类， Texture类

BranchGroup类

一个BranchGroup作为一个场景图分支的根。

BranchGroup对象是唯一能插入到一个Locale对象中的对象。

以BranchGroup节点为根的场景图子图是一个编辑单元。

TransformGroup类

TransformGroup节点通过Transform3D对象定义了一个唯一的3D空间坐标变换，该变换可对其子节点进行位置、方向及比例变换。

GeometryArray类

GeometryArray类是PointArray类，LineArray类，TriangleArray类，QuadArray类， GeometryStripArray类，IndexedGeometryArray类的直接父类

GeometryArray类的对象中包含独立的位置坐标数组、颜色数组、法向量数组、纹理坐标数组和顶点属性。

在数组中的所有颜色值必须在[0.0,1.0]范围内。所有法向量必须是模长为1的单位向量。

PointArray类

PointArray类是组织与定义点的数组类。

PointAttributes类

PointAttributes类的对象用来定义点的各种属性。

点属性包括：

Size：定义点的大小，以像素为单位

Antialiasing：反走样，使外形接近于一个圆形

IndexedPointArray类

从定义好的所有点的坐标与颜色数组中选择出一部分点进行显示。

IndexedLineArray类

从定义好的所有线的坐标与颜色数组中选择出一部分线进行显示。

IndexedTriangleArray类

从给定的顶点中选择出一定数量的顶点，允许顶点重复，形成若干三角形。

IndexedQuadArray类

从给定的顶点中选择出一定数量的顶点，允许顶点重复，形成若干四边面。

LineArray类

LineArray类生成的线段是不连续的，线段的连接方式：0-1，2-3，4-5等，其中，1、2之间与3、4之间不连接。

LineAttributes类

LineAttributes类定义所有与线的显示相关的属性与状态。

LineStripArray类

将定义好的数据点分组，然后分别连成几段连续的线段，分成几个组，就连成几条带（几个Strip）。各条带之间互不连接。

PolygonAttributes类

PolygonAttributes类用来定义多边形显示时的相关属性。这些基本多边形包括三角形、三角形带、三角形扇、四边形。

多边形的三种显示模式：以点的方式显示、轮廓线方式显示、填充多边形方式显示

POLYGON_POINT：多边形以顶点方式显示，则只显示所有顶点。

POLYGON_LINE：多边形以线方式显示

POLYGON_FILL：以填充的多边形面的方式显示，这种模式是默认显示模式。

TriangleArray类

三角面TriangleArray类以一维顶点数组给出顶点的坐标值，从前向后依次以3个顶点形成一个三角形，并且上一个三角形与下一个三角形之间没有公用顶点。

TriangleStripArray类

三角带。stripVertexCounts数组的大小表示分为几个子三角形Strip带。两个Strip之间没有公用顶点。在同一个三角形Strip内，所有三角形都相互连接在一起的，相邻的三角形之间有公共边。用这种方式生成的曲面具有指向相同侧的法向量。

TriangleFanArray类

三角扇。在组织三角形时，以第一个顶点为公用顶点，依次与其余顶点分别连接形成三角形。用这种方法生成的一系列三角形公用第一个顶点。其中给定的顶点数最少为3个。所有三角形具有指向同侧的法向量。

QuadArray类

四边面。QuadArray类以顶点坐标数组中给出的一维顶点数组，从前向后依次以4个顶点形成一个四边形面，并且相邻两个四边形面之间没有公用顶点。给定的总的顶点数必须是4的倍数。

ColoringAttributes类

ColoringAttributes类定义所选择的颜色与光照模型（阴影模型）。

Material类

Material类的对象定义一个三维物体在光照情况下的外观。

如果在一个Appearance类的对象中的Material类的对象一项为null，则光照效果对所有包含该Appearance类的对象的节点不起作用。

包含于Appearance类

环境光颜色Ambient color

散射光颜色Diffuse color

镜面反射光颜色Specular color

物体放射的光颜色Emissive color

物体的发亮特性Shininess

颜色靶子Color target

TransparencyAttributes类

TransparencyAttributes类的对象定义所有几何体透明度的属性。

Light类

该类为抽象类，其中定义的一组参数属性所有类型的光。这些参数包括光颜色、光照开关标志和一个光的作用范围

光源的类型包括平行光源、点光源、环境光

PointLight类

点光源PointLight类在三维空间的一个固定点上定义一种衰减的光源，该类光源从光发出点出发，在所有方向的辐射是相等的。

一个点光源通过其衰减系数反映其衰减，该衰减随着距光源中心距离的增加而增加。

点光源的衰减系数：固定衰减、线性衰减、二次方衰减

DirectionalLight类

平行光源。DirectionalLight类定义了一种光源在无限远处有方向的光

AmbientLight类

环境光源。环境光源是指来自于所有方向的一种光源。

Vector3f类

Vector3f类是一个包含有3个单精度浮点元素x,y,z的向量。如果该向量表示一个法向量，则该向量应该单位化为一个单位向量。

Transform3D类

Transform3D类的对象是一种内部表达为4x4的双精度类型的矩阵，该矩阵是以行的方式存放的。一个Transform3D类的对象用来执行平移、旋转、变比例等坐标变换。

TransformGroup类及其与Transform3D类之间的关系

多个Transform3D对象的组合形成一个总的坐标变换矩阵。

所有表示各种几何变换的Transform3D类的对象必须包含在一个TransformGroup类的对象中，表示对在该TransformGroup类的对象中的三维图形所进行的坐标变换。

如果表示一种几何变换的Transform3D对象没有加入到该TransformGroup类的对象中，则该变换对在该TransformGroup类的对象中的三维图形不起作用。
可以一次定义一个总的坐标变换矩阵，并以此创建一个Transform3D对象，将该Transform3D对象加入到TransformGroup类的对象中。
也可以分步定义多个不同类型的坐标变换矩阵，然后依次创建多个Transform3D对象，每个Transform3D对象表示一种坐标变换，将这些Transform3D对象依次加入到一个TransformGroup类的对象中，则以Transform3D对象的加入次序，依次对三维图形进行变换，Java 3D系统形成最后总的坐标变换。
如果在一个TransformGroup节点中没有定义任何的坐标变换，也就是没有加入任何的Transform3D对象，则该TransformGroup节点拥有一个缺省的4*4坐标变换矩阵，但该矩阵为单位矩阵，表示对几何体不进行任何几何变换。

基础概念

线架模型(Wire Frame)：以线段、圆弧和一些简单的曲线来表示一个三维模型。

Brep边界面模型(Boundary Representation)：将一个封闭的几何体模型所使用的多边形面称为该几何体的Brep边界面。所有的多面体模型都是一种Brep边界面模型。

非均匀有理B样条曲面Non Uniform Rational B-Spline(NURBS)

曲面几何模型的特点是光滑的曲面表示，现在多数曲面几何模型以非均匀有理B样条曲面为基础

在Brep边界面表示中最常用的数据结构：翼边数据结构、半边数据结构

Solid实体

Solid实体几何模型主要通过组成该几何体的边界面所形成的半空间来表示一个物体。物体内部的所有属性都是相同的。

CSG构造实体几何(Constructive Solid Geometry)

通过简单实体(如立方体﹑圆柱体、球体﹑圆锥体、扫描表示法产生的体等)之间的正则布尔运算生成比较复杂的体。其用一种二叉树结构来表示相关实体以及相关的并、交、差布尔运算操作。

CSG树只反映了物体的构造过程与方式，并不反映实体的面、边、顶点等几何信息及其之间关系。因此，这种表示又称为实体的隐式模型或过程模型

VOXEL体素模型(Volume Element)

三维图形显示的最小单元

规则体素空间是将一个立方体分别沿x、y、z轴进行等间距均匀分割所形成的，每一个体素都是一个小立方体。小立方体的中心点称为立方体的格点。

体素与体素之间的连接关系有3种：6连通、18连通、26连通

DEXEL深度元素模型(Depth Element)

DEXEL模型就是用一射线与一个几何体的Brep边界面模型求交，两交点之间属于几何体内部的这段线段称为DEXEL。对于DEXEL模型,通常用一组群到三组群的射线组与几何体的交点来表示一个几何体。

优点：只需要存储射线组群的交点坐标，可以大大压缩存储空间，并且布尔运算是DEXEL线段间的线性运算，运算速度快、精度高。

缺点：失去了每个体素的所拥有的属性信息。

因此DEXEL模型和VOXEL模型之间可相互转换。

Java3D高分辨率大尺度坐标系

32个字节，即256个二进制位的定点数来表示一个数

默认情况下Java3D的坐标系

默认情况下，Java 3D坐标系采用右手坐标系统，坐标系原点在显示器的中心，x轴水平向右，y轴垂直向上，z轴指向观察者。默认情况下，坐标单位为米。

如图所示：

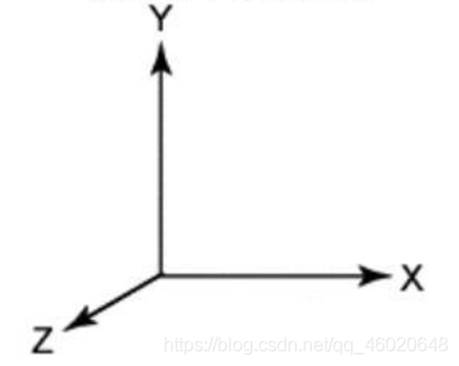
P34页的图

包含谁，谁能加到谁里面？

多边形可视化填充算法

种子填色算法

种子填色算法首先在要填充的多边形区域内选择一个填色种子点( Seed Point)，然后以该种子点为基础，通过与多边形边界的像素点相比较进行填色。

种子填色算法主要有四邻法（如左图）和八邻法（如右图）：

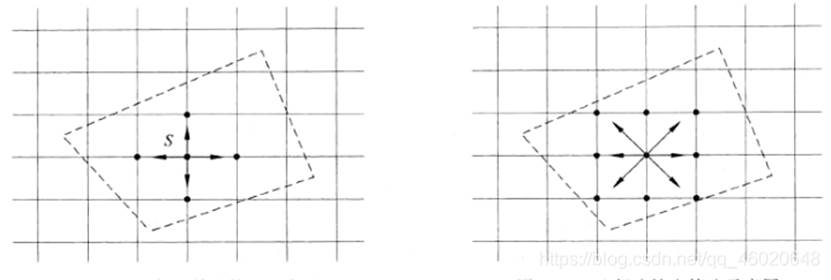
四邻法所走的填充路线为：上、下、左、右。在填充时要判断当前填充象素点与

边界象素点之间的关系。如果要填充的象素点在多边形的边界之内，则进⾏填充；

如果要填充的象素点在多边形的边界之外，则不填充；如果要填充的象素点正好

在多边形的边界上，则保留边界象素点颜色。

八邻法所⾛的填充路线为：上、下、左、右、左上、左下、右上、右下。在填充

时要判断当前填充象素点与边界象素点之间的关系

扫描线填色算法(Scan-Line Filling)

每一条扫描线从上向下以一个像素单位为间隔逐次向下扫描。对每一条扫描线与多边形求交。将交点按x值从小到大排序。用奇偶计数法判断多边形内部的点对。

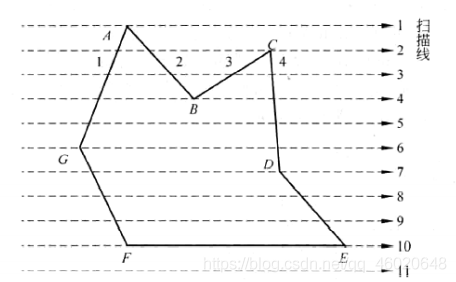
出现点重合时采取的处理方法：

1首先按照多边形顶点顺时针方向标明：A、B、C、D、E、F、G

2扫描线6：扫描到3个顶点，G点处两点重合，按奇偶计数法会出现错误。于是将入线FG的G点的y轴坐标向下移动1个像素单位（我理解为逆时针方向）。

3扫描线7：扫描到3个顶点，D点处两点重合，按奇偶计数法会出现错误。于是将入线CD的D点的y轴坐标向上移动1个像素单位（我理解为逆时针方向）。

如果判断出多边形中有水平边，则将该水平边首先画出，不用求该边与扫描线的交点。

三次Bezier曲线及其性质

端点性质

C(0)=P0, C(1)=Pn

该性质说明一段Bezier曲线通过其首与末控制顶点

端点的切线矢量（详细见书）
Bezier曲线的端点曲率（详细见书）
对称性

对于一段Bezier曲线及其控制顶点，若保持原全部控制顶点的位置不变，只把控制顶点次序编号颠倒过来，则新生成的这段Bezier曲线形状不变，但参数的增长方向相反。

凸包性

一段Bezier曲线严格地位于其控制多边形形成的凸包之内。

变差缩减性

对于一段平面Bezier曲线C(u)，平面内任意一条直线与其交点的个数不多于该直线与其控制多边形的交点个数。

Bezier曲线、曲面拼接的连续性

（1）C0连续：0阶参数连续，第一段曲线的终点与第二段曲线的起点位置重合。

（2）C1连续：一阶参数连续，两相拼接的曲线在拼接点处重合，拼接处有相同的一阶导数。

（3）C2连续：二阶参数连续，两相拼接的曲线在拼接点处重合，拼接处有相同的一阶导数和二阶导数。

（4）G0连续：0阶几何连续，第一段曲线的终点与第二段曲线的起点位置重合，称为G0连续，同时也是C0连续。

（5）G1连续：1阶几何连续，两相拼接的曲线在拼接点处重合，切线方向相同，但大小不等。

（6）G2连续：2阶几何连续，两相拼接的曲线段在拼接点处重合，在拼接点处C0连续、C1连续，在拼接点处二阶导数方向相同，但大小不等。

曲线、曲面的G0（或C0）拼接可保证曲线、曲面在拼接点处是连接在一起的。

曲线、曲面的G1（或C1）拼接可保证曲线、曲面在拼接点处是光顺的。

Bezier曲面的性质-F

（1）端点性质

Bezier曲面的4个角点与控制多边形网格的4个角控制顶点重合。

（2）边界线

Bezier曲面S(u,v)的4条边界线S(0,v)、S(1,v)、S(u,0)、S(u,1)分别由对应的控制网格的4条边界控制多边形形成。

（3）曲面端点的切平面

由通过该端点的两个控制多边形的边所形成的平面和Bezier曲面在该端点的切平面重合。例如，对于曲面角点S(0,0)，切平面为控制顶点P0，0、P0，1、P1，0所形成的平面。

（4）凸包性

Bezier曲面位于其控制网格所形成的凸包之内。

（5）变差递减性

空间任意条直线与Bezier曲面交点的个数不多于该直线与其控制多边形网格的交点个数。

隐藏线、隐藏面消除算法

通常面向视点的所有边都是可见的，将这些边画出来。被前面的可见面隐藏的所有边都是不可见的，不用将这些画出来，或者画成虚线形式。以这种方式显示的形体和用眼睛看到的三维物品相同。将这种消除所有隐藏边的算法称为隐藏线消除算法。

当给定视点与观察方向后，对视点来讲，并不是所有的面都可见，可见面是由视点与观察方向及面的法向量决定。只需显示可见的面，无须显示隐藏的面，这种算法叫做隐藏面消除算法。

隐藏面的消除与隐藏线消除有时是相互关联的。由隐藏线所围成的面是隐藏面，两个隐藏面所共有的线为隐藏线。

Z Buffer隐藏面消除算法

在显示器的像素点阵建立两种缓冲存储单元阵列：Z Buffer 和C Buffer阵列。

从视点出发通过每个像素点发出一条射线，Z Buffer阵列存储距离视点最近的多边形与射线交点z坐标，C Buffer阵列存储对应的交点所在面颜色。

区域排序消隐算法

区域排序消隐算法就是在图像空间中，将组成几何体的所有多边形按照z坐标深度值从小到大排序，然后用前面的可见多边形去切割后面的多边形，将后面的多边形切割为可见与不可见两部分，最后将所有可见多边形显示出来，就为几何体消隐后的图像。

最小包围矩形、最小包围圆

用对边分别平行于两个坐标轴的边形成一个最小包围矩形

求法如下：求所有几何数据点的最小x、y值与最大x、y值，则由这两点定义的平行于两坐标轴的矩形就是最小包围矩形

最小包围盒、最小包围球

最小包围盒指用三对分别平行于坐标平面的最小六面体（长方体）包围一个三维几何体。最小包围盒是指该六面体正好包围该三维几何体，在所有包围该三维几何体的六面体中，它是最小的。

同一平面内点与多边形的包含判定算法-F

凸多边形的叉积判断法

首先假定按逆时针方向计算的叉积为正，则按顺时针⽅向计算的叉积为负。从给定的一个点向多边形的各个顶点做向量。然后，按顶点顺序逐个计算每相邻两向量之间的叉积。如果所有的叉积符号相同，说明点在多边形内；反之，则在多边形外。（右手螺旋定则：逆正顺反）

补充：

叉积的一个重要性质是可以通过它的符号判断两矢量相互之间的顺逆时针关系：

若 P × Q > 0 , 则P在Q的顺时针方向

若 P × Q < 0 , 则P在Q的逆时针方向

若 P × Q = 0 , 则P与Q共线，但可能同向也可能反向）

夹角之和检验法

首先将要判断的点与多边形的各个顶点依次连接形成一系列向量，然后按照顶点顺序求相邻两向量之间的夹角。假定按逆时针方向计算的角度为正，按顺时针方向计算的角度为负。如果所有的夹角符号相同（或和为360度），说明点在多边形内；反之，则在多边形外。

交点计数检验法

从要判断的点向右做一条射线，求出射线与多边形交点的个数。如果交点的个数是奇数，则点在多边形内；反之，则在多边形外。（奇内偶外，同2异1）

局部光照明计算模型

环境光部分计算

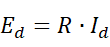
Ed表示P点所反射的环境光的强度

R为P点的漫反射系数（介于0和1之间）

Id为照射在P点的入射环境光的强度

直射光强度计算

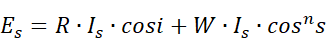
Es表示直射光反射的总光强

Is为直射光的入射光强

R为P点的漫反射系数（介于0和1之间）

W为P点的镜面反射系数，介于0和1之间

i为直射光在P点与法向量的夹角

n为控制高光聚散的系数，它与P点的材料有关

透射光强度计算

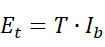
Et为从几何体内部经几何体表面P点处透射出的光强度

T为P点的透射系数（取值介于0到1之间）

Ib为从物体内部到达几何体表面P点处的入射光强度

P点处总的光强度计算

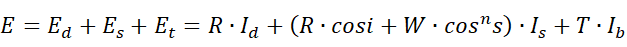
Gouraud算法和Phong算法及区别-F

Gouraud算法

首先计算各个平⾯多边形的法向量，由该法向量确定各个多边形顶点处的单位法向量，再由每个顶点的单位法向量通过向量合成方式计算各公共顶点的单位法向量；然后应用局部光照明模型计算各多边形顶点处的光颜色、光强度值，通过对各多边形顶点的光颜⾊、光强度值的线性插值求出多边形边及内部所有点的光颜色、光强度值。

Gouraud 算法的优点是计算量小。

Gouraud 算法的缺点：高光区域有时会出现异常；当对曲面用不同的多边形进行分割时会产生不同的显示效果；Gouraud明暗处理会造成表面上出现过亮或过暗的条纹，称为马赫带（Mach_band）效应。

Phong 算法

首先计算各个平面多边形的法向量，由该法向量确定各个多边形顶点处的单位法向量，再由每个顶点的单位法向量通过向量合成方式计算各公共顶点的单位法向量；通过对平面多边形各顶点的法向量进行双线性插值，计算出平面多边形内部各点的法向量；再由所有这些点的法向量，通过局部光照模型计算平面多边形内部所有点的光颜色与光强度值。

Phone 算法的优点：Phong 算法显示的图形比Gouraud 算法更真实，能够产生正确的高光区域；

缺点：由于是先计算出平面上各点的法向量，然后再计算各点的光强度，所以 Phong 算法计算量远大于 Gouraud 算法；针对某些多边形分割的曲面，Phong 算法不如 Gouraud 算法好

Whitted整体光照明模型

计算公式及各参数的含义

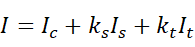
Ic：通过局部光照明模型计算出的光强度，也可采⽤ Phong 模型计算。

Is：为来⾃于其它⼏何体的镜⾯反射⽅向的⼊射光强度。

kS：为镜⾯反射系数，为 0～1 之间⼀个常数。

It：为来⾃于其它⼏何体的折射⽅向光强。

kt：为透射系数，是 0～1 之间的常数。

Whitted 光照模型是⼀个递归的计算模型。

光线追踪算法

光线追踪算法是一种在由多光源与多个几何体组成的场景中，对几何体进行消隐与整体光强度计算的算法。光线追踪算法沿着到达视点的光线的反方向进行跟踪，经过屏幕上每一个像素点，找出所跟踪的光线与几何体的交点，在该交点处分别沿反射方向与折射方向再进行跟踪，找出影响该点光强度的所有光源，通过迭代、累加计算跟踪点的光颜色与光强度。

私聊博主获取打印版，^_^