点击此链接进行红黑树模拟

前言

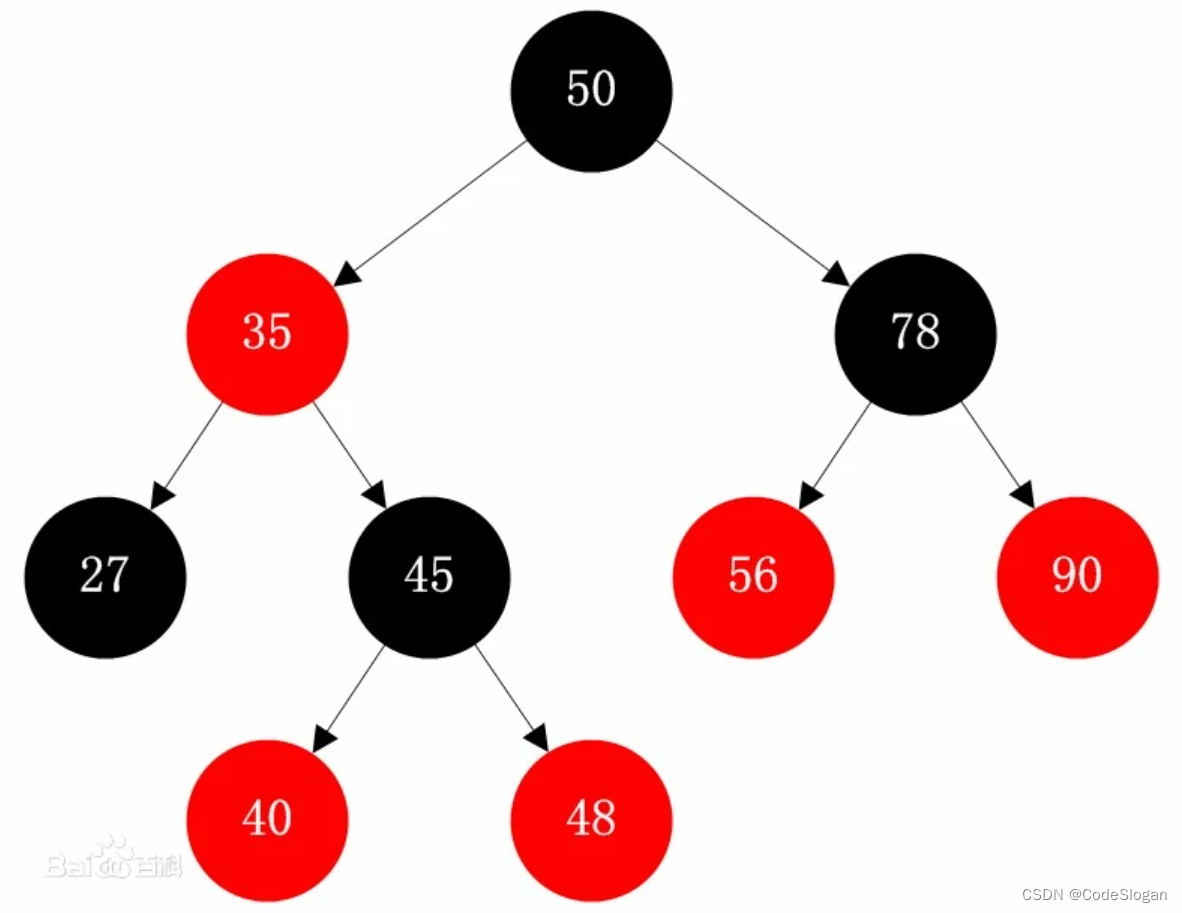
所有的红黑树的插入删除操作都与二叉搜索树（BST）的操作类似，只不过红黑树在BST的基础上，多出了维护红黑树性质的操作。而红黑树的性质有以下5条：

  1. 所有的结点要么红，要么黑
  2. 根结点必为黑
  3. 叶子结点（NULL结点）全为黑
  4. 任意两个红色结点必不相邻
  5. 任意结点往下到任意叶子结点的简单路径上所包含的黑点个数相同

插入

（看叔叔结点的脸色）
待插入的结点默认是红色。因为如果是黑色，每插入一个结点，由于路径上的黑色结点数会发生改变，就要进行调整；如果默认是红色的话，只有当出现两个相邻连续的红色结点时，才要进行调整

  • 待插入的结点是树的根结点，则染成黑色
  • 待插入的结点的父结点是黑色，则此时满足红黑树的性质，不用做出任何改变
  • 待插入的结点的父结点是红色（爷结点必然为黑色），此时要考虑其叔叔结点的颜色
    • 如果叔叔结点也是红色，则把父结点和叔叔结点染成黑色，爷结点染成红色；再把当前结点设置为爷结点，继续上述操作，直至根结点，相当于往上递归
    • 如果叔叔结点是黑色，则需要进行旋转操作。如果待插入的结点是父结点的右孩子，则要先进行左旋，转换为是左孩子的情况（如果在右边，则孩子应该旋转至靠右的情况）。然后再父结点为中心，进行右旋，此时父结点会成为这个区域最上面的那一个结点；同时，交换父结点和爷结点的颜色。这样就解决了因为插入导致两个相邻红色结点的情况

删除

回顾BST的删除操作，主要可以归为三类。

  1. 所删除的结点无左右孩子，直接删除即可
  2. 所删除的结点只有左（右）孩子其中一个，删除该结点，但该结点的颜色被其左或右孩子继承（这点在RBT删除操作中非常常见， 一个结点虽然被删除了，但是它的颜色将会在那个位置上保留下来）
  3. 所删除的结点同时拥有左右孩子，则默认找该结点的后继结点来代替这一结点，完成逻辑上的删除，从而转换成删除该后继结点，进而转换成情况一或二

基于以上分析，对于RBT的删除操作，我们只用讨论其无左右孩子，或者只有一个左右孩子的情况。
接着我们讨论如何维护颜色

  • 当删除的结点为黑色且只有一个左右孩子，这里只用讨论其孩子为红色的情况（因为其它情况可以统一归为第三类讨论），孩子继承其父结点的黑色
  • 当删除的结点为红色且无孩子时，直接删除即可，因为不会改变性质
  • 当删除的结点为黑色且无孩子时，或者有一个为黑色的孩子，那么此时该位置会产生一个双黑结点（这是为了维护性质5）

那么我们的问题就进一步转换成了如何消除这个双黑结点（维护性质1）
（看兄弟结点的脸色，一个大的目标就是要把兄弟结点染成黑色，兄弟结点的右孩子染成红色）
首先如果该位置的兄弟结点为红色（父结点必为黑），交换兄弟结点与父结点的颜色，同时左旋。这样就把该位置的兄弟结点变为了黑色，这样就转换成了下面的情况。
如果该位置的兄弟结点为黑色，此时就要考虑它的两个孩子的颜色。根据排列组合，它的两个孩子会出现4种情况，分别为黑红、红红、红黑、黑黑。其中，黑红、红红可以归为一类讨论，所以我们的工作量就是讨论三类情况

  1. 黑黑。解决问题的状态。此时当前结点为双黑结点，兄弟结点也为黑。把当前结点和兄弟结点同时褪掉一层黑色，则当前结点变为普通的黑色结点，兄弟结点变为红色结点。但是为了维护性质5，我们要在父结点上加上一重黑色，如果父亲结点原来为红色，那么加上一重黑色后，当前循环终止；如果父亲结点原来为黑色，则会变为双黑结点。这个操作一句话解释就是：把双黑的情况往上传导，直至根结点
  2. 红黑。这是一种过渡状态（不能最终解决问题）。兄弟结点的右孩子为黑色，我们目标是把其染成红色，具体操作如下：交换兄弟结点与其左孩子的颜色，同时将兄弟结点右旋。这样就转换成了右孩子是红色的情况。
  3. 黑红、红红。解决问题的状态。此时父结点的颜色是未知的，什么颜色都可以，不影响。交换父结点与兄弟结点的颜色，同时将右孩子从红色染成黑色，然后将兄弟结点左旋。这样就成功把双黑结点消成普通黑色结点

能阅读到这里，说明你还是认可我的笔记的，希望对你有用！！

参考资料

  1. AcWing Y总1小时搞定红黑树
  2. 王道408-2023年数据结构考研复习指导
  3. 对红黑树的认识总结-张彦峰ZYF