前言

本文记录了在跟随李沐老师的动手学深度学习课程中，CNN部分的要点

“卷积神经网络（convolutional neural network，CNN）是一类强大的、为处理图像数据而设计的神经网络。 基于卷积神经网络架构的模型在计算机视觉领域中已经占主导地位，当今几乎所有的图像识别、目标检测或语义分割相关的学术竞赛和商业应用都以这种方法为基础。”——李沐

数学上的卷积

在数学中，两个函数（比如f,g:Rd→Rf, g: \mathbb{R}^d \to \mathbb{R}）之间的“卷积”被定义为

(f∗g)(x)=∫f(z)g(x−z)dz.(f * g)(\mathbf{x}) = \int f(\mathbf{z}) g(\mathbf{x}-\mathbf{z}) d\mathbf{z}.

卷积是当把一个函数“翻转”并移位x\mathbf{x}时，测量ff和gg之间的重叠。

当为离散对象时，积分就变成求和。例如：对于由索引为Z\mathbb{Z}的、平方可和的、无限维向量集合中抽取的向量，我们得到以下定义：

(f∗g)(i)=∑af(a)g(i−a).(f * g)(i) = \sum_a f(a) g(i-a).

卷积层

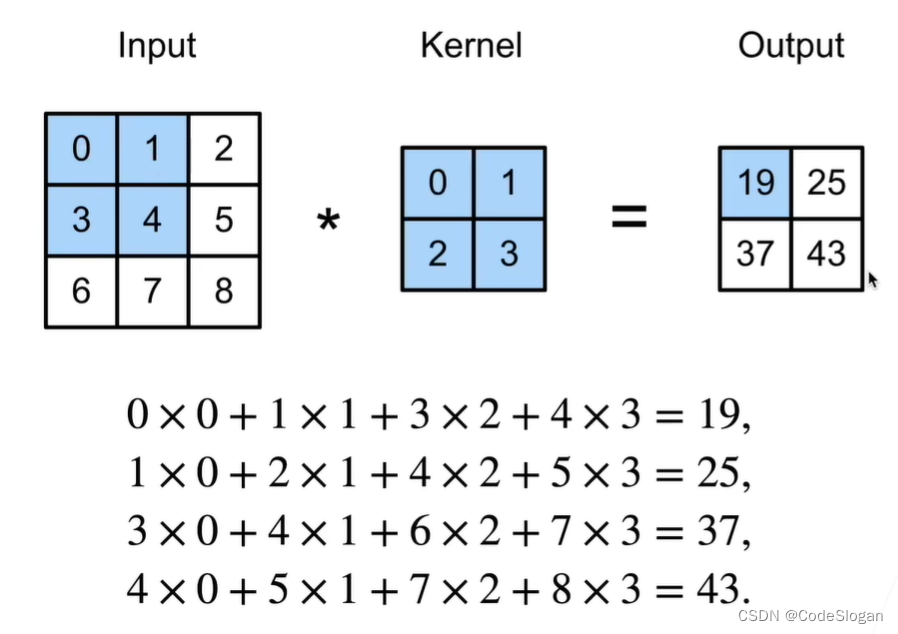
卷积层将输入与核矩阵进行交叉相关，加上偏移后得到输出

  1. 核矩阵和偏移是可学习的参数
  2. 核矩阵的大小是超参数

因为卷积核的存在，CNN的参数不会像全连接神经网络那样，随着输入的增加，而使得参数变得巨大导致无法训练

两个原则：

  • 平移不变性：识别器不会因为要识别图片的位置不同，而发生改变。体现在卷积核不变

hi,j=∑a,bvi,j,a,bxi+a,j+bh_{i,j}=\sum_{a,b} v_{i,j,a,b}x_{i+a,j+b}

  • 局部性：需局部而非全局信息。体现在卷积核的大小

hi,j=∑a=−ΔΔ∑b=−ΔΔva,bxi+a,j+bh_{i,j}=\sum_{a=-\Delta}^{\Delta} \sum_{b=-\Delta}^{ \Delta}v_{a,b}x_{i+a,j+b}

二维交叉相关：

（卷积核作为CNN当中的参数，体现了平移不变性）

图像卷积，代码实现

1
2
3
4
5
6
7
8
def corr2d(X, K):  #@save
    """计算二维互相关运算，即上图中的操作"""
    h, w = K.shape  # 得到卷积核的大小
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))  # 定义卷积运算后的大小
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

填充与步幅

两者都是卷积层的超参数

填充padding：将被卷积核卷积运算后的结果，通过在周围添加额外的行 / 列，填充回原来的形状

填充 php_h 行和 pwp_w 列，输出形状为

(nh−kh+ph+1)∗(nw−kw+pw+1)(n_h-k_h+p_h+1)*(n_w-k_w+p_w+1)

步幅stride：指行、列的滑动步长，可以成倍的减少输出形状。在前面的计算中，步幅默认为1，这会导致需要大量的计算才能得到较小的输出

通常，当垂直步幅为shs_h、水平步幅为sws_w时，输出形状为

⌊(nh−kh+ph+sh)/sh⌋×⌊(nw−kw+pw+sw)/sw⌋.\lfloor(n_h-k_h+p_h+s_h)/s_h\rfloor \times \lfloor(n_w-k_w+p_w+s_w)/s_w\rfloor.

多输入多输出通道

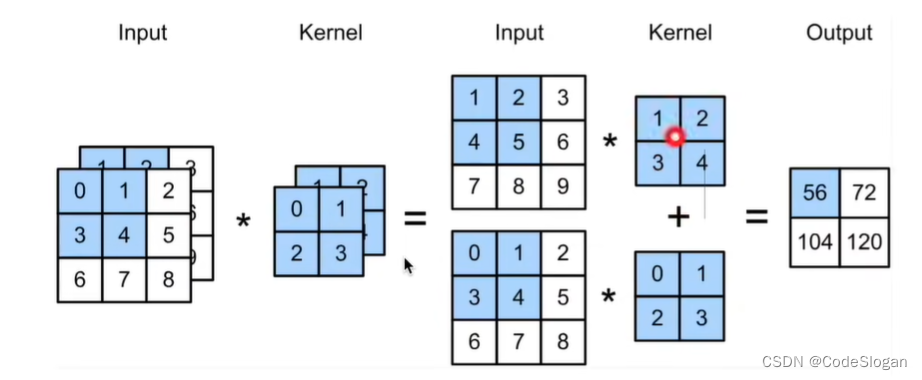
多输入通道

多个输入通道，出现在RGB三原色

  • 让每个通道都有个卷积核，结果是所有卷积操作结果的和

多输出通道

每个输出通道可以识别特定的模式。这一层的输出作为下一层的输入，输入通道组合输入中的模式

1x1卷积层：调整网络层的通道数量（通道融合）和控制模型复杂性

池化层

类比成和卷积层一样有个卷积核，但核内做的不是卷积操作
而是返回滑动窗口中的最大值

  • 池化有最大池化与平均池化
  • 降低卷积层对位置的敏感性，照顾平移不变性这一特点，池化层允许像素出现一定程度的偏移（如何理解？）
  • 有窗口大小、填充、步幅作为超参数
1
2
3
4
5
6
7
8
9
10
def pool2d(X, pool_size, mode='max'):
    p_h, p_w = pool_size
    Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()  # 最大
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()  # 平均
    return Y

LeNet

先使用卷积层来学习图片的空间信息，然后使用全连接层来转换到类别空间

用卷积层代替MLP的另一个好处是：模型更简洁、所需的参数更少

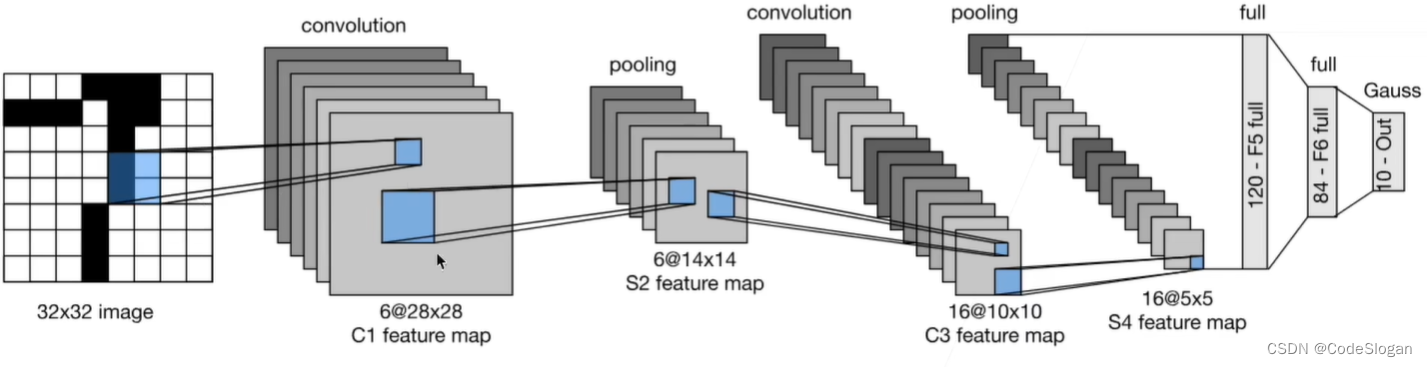
LeNet
逐渐地把空间（高宽）变小，通道变多

1
2
3
4
5
6
7
8
9
10
#  LeNet网络模型实现
net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

网络由两个部分组成：

  • 卷积编码器：由2个卷积层组成
  • 全连接层密集块：由3个全连接层组成

现代经典网络

以下记录的网络模型为CNN的变种，是十分经典的模型

AlexNet

深度卷积神经网络。可以理解为更深更大的LeNet。能够学习更大的图片

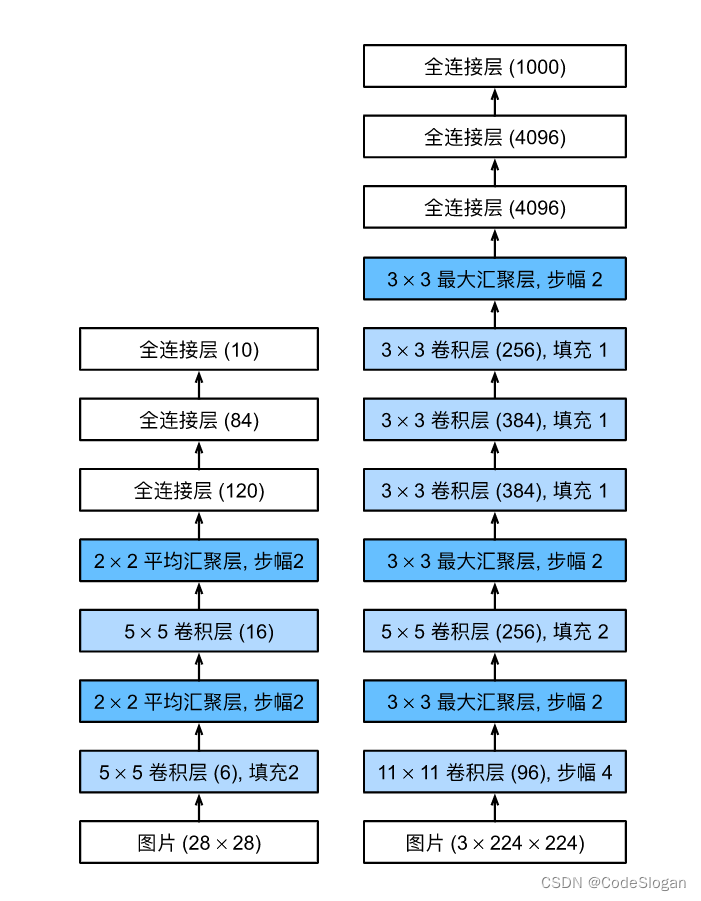
LeNet与AlexNet网络对比：

AlexNet由八层组成：五个卷积层、两个全连接隐藏层和一个全连接输出层。 其次，AlexNet使用ReLU而不是sigmoid作为其激活函数。

主要改进：

  • Dropout。因模型过大，用其做正则
  • ReLU。减缓梯度消失
  • MaxPooling
  • 数据增强

内部结构：

  1. 在网络的第一卷积层，使用了一个11*11的更大窗口（卷积核）来捕捉对象。同时，步幅为4，以减少输出的高度和宽度。另外，输出通道的数目远大于LeNet
  2. 使用三个连续的卷积层和较小的卷积窗口。除了最后的卷积层，输出通道的数量进一步增加。在前两个卷积层之后，汇聚层不用于减少输入的高度和宽度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#  AlexNet实现
net = nn.Sequential(
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Flatten(),
    # 这里，全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
    nn.Linear(6400, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    # 最后是输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
    nn.Linear(4096, 10))

VGG

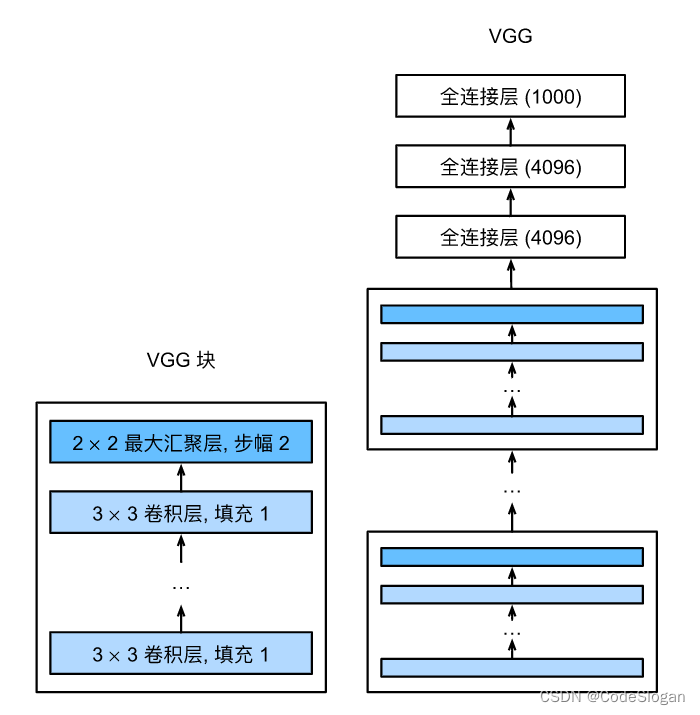
使用块的网络VGG，更大更深的AlexNet
块的使用导致网络定义的非常简洁。使用块可以有效地设计复杂的网络。

VGG块网络模型的思想会应用到后续的一系列网络中

  • VGG使用可复用的卷积块来构建深度卷积神经网络。不同的VGG模型可通过每个块中卷积层数量和输出通道数量的差异来定义。
  • 不同的卷积块个数和超参数可以得到不同复杂度的变种

如下函数可以构造出一个卷积块，其中包含了若个干卷积层+激活函数，最后再补一个池化层。将这三者绑定在一个块中，批量生成

实现一个VGG块：

1
2
3
4
5
6
7
8
9
10
#  卷积层的数量、输入通道的数量、输出通道的数量
def vgg_block(num_convs, in_channels, out_channels):
    layers = []
    for _ in range(num_convs):
        layers.append(nn.Conv2d(in_channels, out_channels,
                                kernel_size=3, padding=1))
        layers.append(nn.ReLU())
        in_channels = out_channels
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    return nn.Sequential(*layers)

NiN

网络中的网络，使用了1x1的卷积层

卷积层需要较少的参数：输入通道x输出通道x核大小。而卷积层后的第一个全连接层需要的参数通常非常大

ci∗co∗k2c_i*c_o*k^2

NiN的出现就是为了解决这个问题，提出不单独使用全连接层

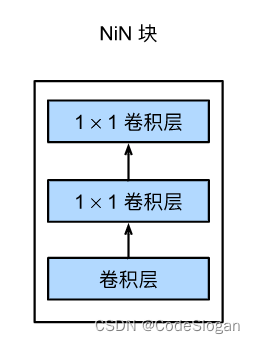
一个NiN块：

  • 一个NiN块为一个卷积层加两个1x1的卷积层（后者分别相当于一个全连接层，对每个像素增加了非线性性）
  • 使用全局AvgPooling层来代替全连接层（不容易过拟合，更少的参数个数）

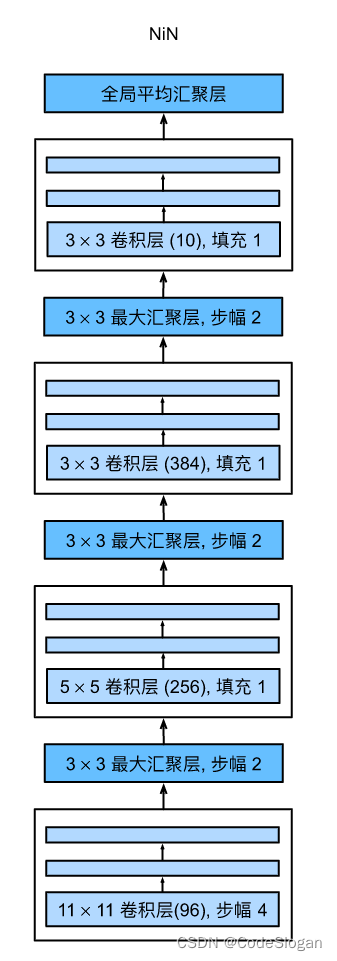
NiN架构：

  1. 无全连接层
  2. 由交替的NiN块和步幅为2的MaxPooing层组成（逐步减少高宽和增加通道路）
  3. 最后使用全局平均池化层得到输出（其输入通道数是类别数）
1
2
3
4
5
6
7
# NiN块
def nin_block(in_channels, out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
        nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# NiN架构
net = nn.Sequential(
    nin_block(1, 96, kernel_size=11, strides=4, padding=0),
    nn.MaxPool2d(3, stride=2),
    nin_block(96, 256, kernel_size=5, strides=1, padding=2),
    nn.MaxPool2d(3, stride=2),
    nin_block(256, 384, kernel_size=3, strides=1, padding=1),
    nn.MaxPool2d(3, stride=2),
    nn.Dropout(0.5),
    # 标签类别数是10
    nin_block(384, 10, kernel_size=3, strides=1, padding=1),
    nn.AdaptiveAvgPool2d((1, 1)),
    # 将四维的输出转成二维的输出，其形状为(批量大小,10)
    nn.Flatten())

GoogleNet

含并行连结的网络，提出了Inception块的概念

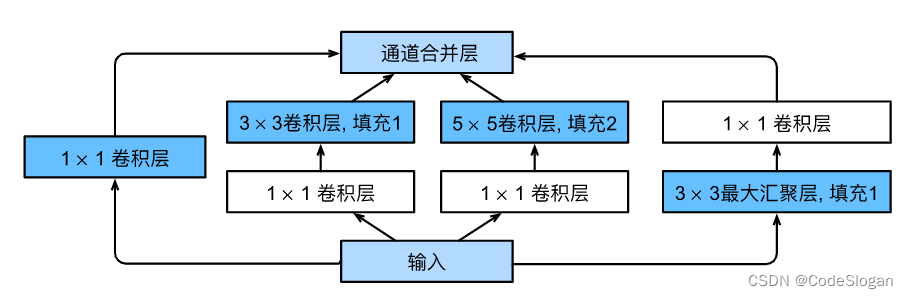
Inception块由4条并行的路径组成：

  1. 前三条路径使用窗口大小为1×11\times 1、3×33\times 3和5×55\times 5的卷积层，从不同空间大小中提取信息
  2. 中间的两条路径在输入上执行1×11\times 1卷积（起到降通道数的作用，从而降低模型的复杂性）
  3. 第四条路径使用3×33\times 3最大汇聚层，然后使用1×11\times 1卷积层来改变通道数
  4. 输出的高宽和输入的一致，只增加了通道数。在Inception块中，通常调整的超参数是每层输出通道数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Inception(nn.Module):
    # c1--c4是每条路径的输出通道数
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # 线路1，单1x1卷积层
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        # 线路2，1x1卷积层后接3x3卷积层
        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1x1卷积层后接5x5卷积层
        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3x3最大汇聚层后接1x1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)

    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        # 在通道维度上连结输出
        return torch.cat((p1, p2, p3, p4), dim=1)
  • Inception块借用了NiN块网络的概念，有4条并行路径的子网络
  • 它通过不同窗口形状的卷积层和最大汇聚层来并行抽取信息，并使用 1×1 卷积层减少每像素级别上的通道维数从而降低模型复杂度
  • GoogLeNet是多个Inception块与其它层（卷积层、全连接层）的组合

ResNet

残差网络。通过残差块构建跨层的数据通道

当层出不穷的网络出现后，人们发现越深的网络模型性能越好。但当网络的层数到达一定极限后，模型的性能不升反降。ResNet的出现解决了这一问题

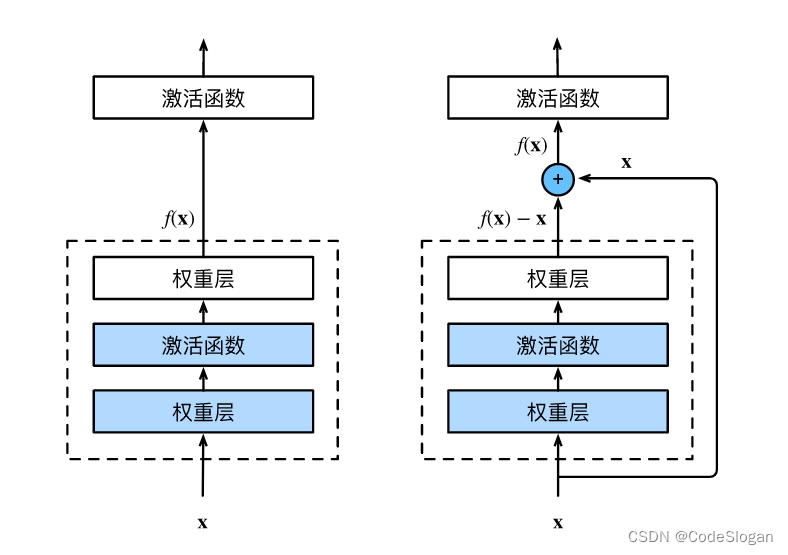
残差网络的核心思想是：每个附加层都应该更容易地包含原始函数作为其元素之一

在残差块中，输入可通过跨层数据线路更快地向前传播

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 残差块实现
class Residual(nn.Module):  #@save
    def __init__(self, input_channels, num_channels, use_1x1conv=False, strides=1):
        super().__init__()
        self.conv1 = nn.Conv2d(input_channels, num_channels,
                               kernel_size=3, padding=1, stride=strides)
        self.conv2 = nn.Conv2d(num_channels, num_channels,
                               kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2d(input_channels, num_channels,
                                   kernel_size=1, stride=strides)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(num_channels)
        self.bn2 = nn.BatchNorm2d(num_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        Y += X
        return F.relu(Y)

ResNet在加深的时候，不会让模型变坏。
在f(x)=x+g(x)f(x)=x+g(x)中，若g(x)g(x)对loss下降没有影响，就会拿不到梯度，对模型的影响会减小

参考资料

  1. 李沐-动手学深度学习视频
  2. 《动手学深度学习》第6章、第7章
  3. 《神经网络与深度学习》邱锡鹏